Greedy Algorithm

Codeforces Round #635 (Div. 2) #C 문제

오늘은 4/15 어제밤에 치뤘던 대회의 greedy algorithm 문제에 대해 소개드리겠습니다.

문제

왕국에는 n개의 도시와 n-1개의 양방향 도로가 있다.
어느 도시에서든, 다른 도시로 가는 길이 존재한다.
도시는 1부터 n까지 번호가 매겨져 있고, 도시 1은 왕국의 수도이다. => (트리 구조)
Linova는 정확히 k개의 도시를 선택하여, 산업도시로 만들것이다.
1년에 한번 수도에서 회의가 열린다. 회의에 참석하기 위해 각 산업도시에서 사절을 보낸다. 모든 사절들은 가장 짧은 경로로 수도로 향한다.
수도로 가는 길에, 각 사절은 그가 가는 길의 관광도시 수 만큼 행복함을 느낀다.
Linova는 모든 사절들의 행복함의 합이 최대가 되도록 k개의 도시를 선택하고 싶어한다.

입력

첫 번째 줄에 두 개의 정수 n(도시의 수)과 k(산업도시 수) $(2≤n≤2⋅10^5, 1≤k<n)$ 가 주어진다.
다음 n-1개의 줄에 각각 두 개의 정수 u와 v $(1≤u,v≤n)$ 가 주어지며, 이는 도시 u와도시 v를 연결하는 도로가 있음을 나타낸다.

출력

모든 사절들의 행복함의 최대 합계를 출력한다.

풀이

우선, 수도(루트 노드)로 가는 사절들의 최단 경로의 길이는, 해당 산업도시의 레벨의 값과 같습니다.

다음의 예제를 트리로 그려봅시다.

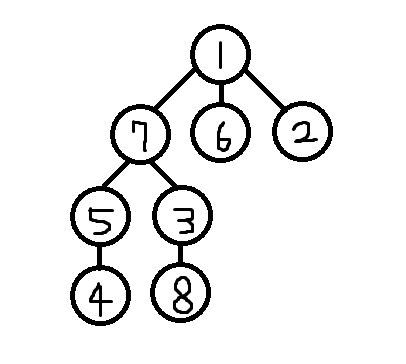
이 상태에서, 각 노드의 레벨은 DFS 로 구현할 수 있습니다.

그 코드입니다.

vector<int> tree[200001];
int lv[200001];

void go(int node, int level, int parent)
{
	lv[node] = level; //현재 자신의 레벨값 저장.
	int size = tree[node].size(); //각 도시와 인접한 도시의 수
	for (int i = 0; i < size; i++)
		if (parent != tree[node][i]) //부모가 아닌 모든 인접 노드(자식 노드)를 방문하면서,
			go(tree[node][i], level + 1, node); //자식 노드이므로 level+1. 그 부모는 현재 자신.
}

이렇게 모든 노드의 레벨을 lv배열에 저장해놓고, 값을 출력해보면 다음과 같습니다.

for (int i = 1; i <= N; i++)
		printf("lv[%d] = %d\n", i, lv[i]);

lv[1] = 0
lv[2] = 1
lv[3] = 2
lv[4] = 3
lv[5] = 2
lv[6] = 1
lv[7] = 1
lv[8] = 3

우리가 원하는 값은 모든 사절들의 행복함의 최대 합계이므로, 매 순간마다 lv값이 가장 큰 도시를 k번 선택합니다. (greedy) 지난시간에 배운 분할정복을 이용한 merge sort 또는 quick sort로 레벨값을 내림차순 정렬한 후 k개 만큼의 합을 구하면 될 듯 합니다. nlogn의 시간복잡도입니다.

C++ 에는nlogn 시간복잡도로 정렬해주는 sort함수가 #include <algorithm> 헤더 파일에 있으므로, 그걸 사용하겠습니다.

#include <cstdio>
#include <vector>
#include <algorithm> // sort()
#include <functional> //greater<>()
#define ll long long
using namespace std;

vector<int> tree[200001];
int lv[200001];

void go(int node, int level, int parent)
{
	lv[node] = level;
	int size = tree[node].size();
	for (int i = 0; i < size; i++)
		if (parent != tree[node][i])
			go(tree[node][i], level + 1, node);
}

int main()
{
	int N, k, u, v;
	scanf("%d %d", &N, &k);
	for (int i = 1; i < N; i++)
	{
		scanf("%d %d", &u, &v);
		//양방향 도로
		tree[u].push_back(v);
		tree[v].push_back(u);
	}

	go(1, 0, 1);
	sort(lv + 1, lv + 1 + N, greater<>()); //내림차순 정렬

	ll ans = 0; //값이 int형 범위를 넘어갈 수 있습니다.
	for (int i = 1; i <= k; i++)
		ans += (ll)lv[i];
	printf("%lld", ans);
	return 0;
}

//출력결과 : 11.

값이 11이 나옵니다. 예제의 답 9와 다르네요.

그 이유에 대해 생각해봅시다.

위의 lv배열을 내림차순으로 정렬하면, {3,3,2,2,1,1,1,0} 이 됩니다. 따라서 k 가 5로 주어졌으므로, 3+3+2+2+1 = 11을 출력한 것입니다. 이 경우를 그림으로 나타내봅시다.

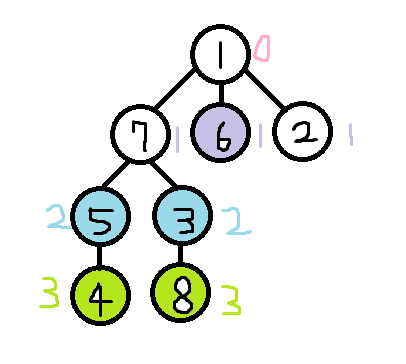
위의 그림에서 4번 도시, 8번 도시를 고를때까진 문제가 없습니다. 하지만 5번 도시와 3번 도시를 고를때,

이 도시들이 관광도시에서 산업도시로 바뀌는 과정에서 4번 사절과 8번 사절의 행복함이 1씩 감소하게됩니다.

그렇다면, x번 도시가 산업도시로 선택됨으로 인해 행복함이 감소되는 사절의 수는 어떻게 구할까요?

그 답은 x번 도시의 자손 노드의 수 입니다. 왜냐하면 우리는 레벨이 높은 도시부터 우선적으로 골라왔기때문에, 어떤 노드를 고를 때 그 자손 노드들은 이미 다 선택되어있을 것입니다. 따라서 다음과 같은 상황이 됩니다.

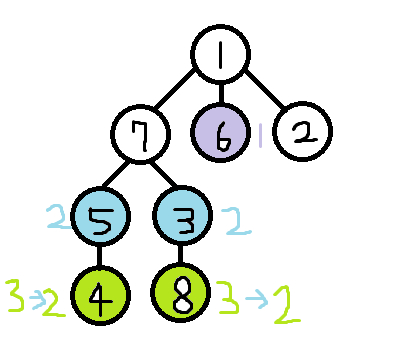
따라서 2+2+2+2+1 = 9로 정확한 답이 됩니다. (위의 그림에서 7을 고른다면 답보다 값이 작아집니다.)

답을 출력하기 위한 과정은 다음과 같습니다.

DFS 과정에서 각 노드의 자손 노드의 수를 저장하는 descendant배열을 만듭니다.
도시 x를 선택할 때 발생하는 행복함의 값은, lv[x] - descendant[x] 입니다. (자손 노드의 수만큼 총 행복함 값이 감소하고, 자신의 lv값 만큼 행복함이 증가하므로)
위의 값이 큰것부터 k개를 뽑아 더한 값을 출력하면 됩니다.(greedy)

그 코드입니다.

#include <cstdio>
#include <vector>
#include <algorithm>
#include <functional>
#define ll long long
using namespace std;

vector<int> tree[200001];
int lv[200001];
int descendant[200001];

int go(int node, int level, int parent)
{
	lv[node] = level;
	int size = tree[node].size(), d = 0;

	for (int i = 0; i < size; i++)
		if (parent != tree[node][i])
		//[현재 자식의 자손 수 + 현재 자식노드(1)]을 모든 자식에 대해 반복 => 현재 노드의 총 자손 수
			d += go(tree[node][i], level + 1, node) + 1;

	return descendant[node] = d;
}

int main()
{
	int N, k, u, v;
	scanf("%d %d", &N, &k);
	for (int i = 1; i < N; i++)
	{
		scanf("%d %d", &u, &v);
		tree[u].push_back(v);
		tree[v].push_back(u);
	}

	go(1, 0, 1);
	for (int i = 1; i <= N; i++)
		lv[i] -= descendant[i];
	sort(lv + 1, lv + 1 + N, greater<>());

	ll ans = 0;
	for (int i = 1; i <= k; i++)
		ans += (ll)lv[i];
	printf("%lld", ans);
	return 0;
}